Your basket is currently empty!
Chinese Whispers Graph Clustering in Python
I needed a simple and efficient unsupervised graph clustering algorithm. MCL is a bit heavy for my needs and I was after something that was available in pure Python (because of environment access and compatibility issues) pretty much immediately. There isn’t exactly a lot of choice! I stumbled across Chinese Whispers an elegant and simple solution. I couldn’t find a simple implementation in Python so I created one myself using the formulas on the original paper. It uses NetworkX (for convenience – you could easily implement without this) and is incredibly fast.
import networkx
# build nodes and edge lists
nodes = [
(1,{'attr1':1}),
(2,{'attr1':1})
...
]
edges = [
(1,2,{'weight': 0.732})
....
]
# initialize the graph
G = nx.Graph()
# Add nodes
G.add_nodes_from(nodes)
# CW needs an arbitrary, unique class for each node before initialisation
# Here I use the ID of the node since I know it's unique
# You could use a random number or a counter or anything really
for n, v in enumerate(nodes):
G.node[n]['class'] = v
# add edges
G.add_edges_from(edges)
# run Chinese Whispers
# I default to 10 iterations. This number is usually low.
# After a certain number (individual to the data set) no further clustering occurs
iterations = 10
for z in range(0,iterations):
gn = G.nodes()
# I randomize the nodes to give me an arbitrary start point
shuffle(gn)
for node in gn:
neighs = G[node]
classes = {}
# do an inventory of the given nodes neighbours and edge weights
for ne in neighs:
if isinstance(ne, int) :
if G.node[ne]['class'] in classes:
classes[G.node[ne]['class']] += G[node][ne]['weight']
else:
classes[G.node[ne]['class']] = G[node][ne]['weight']
# find the class with the highest edge weight sum
max = 0
maxclass = 0
for c in classes:
if classes[c] > max:
max = classes[c]
maxclass = c
# set the class of target node to the winning local class
G.node[node]['class'] = maxclass
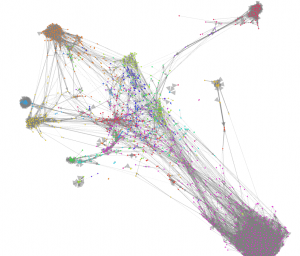
Given its simplicity it’s a remarkably effective algorithm. The image below shows a Gephi visualisation using the ForceAtlas2 algorithm. The node colours show the clusters identified by CW.
As you can see, the two algorithms broadly agree. CW took seconds to run whereas Gephi taxed my CPU to the max for many minutes (actually I think it was 10’s of minutes).
If you can fit you data into a graphical form, this is a very viable alternative to K-means style clustering, made even more attractive (for certain tasks) by the fact that it’s parameter free and thus you don’t need to pre-define the number of clusters (the bane of many a data scientist). It just finds the clusters that are there. This is, of course, also a draw-back in some circumstances. For example, if your data is heavily interlinked (a high degree to cardinality ratio) with no natural subgraphs, CW may just find a single cluster where you can demand K-means go find some. You can get around this to extent by relaxing your edge weight threshold (i.e. induce a subgraph with only edge weights greater than a threshold, then cluster that) an approach prone to graph fragmentation, which may or may not be desirable. It’s also prone to finding micro-clusters which in many cases could be construed as noise.
For my purposes it works incredibly well and I assume scales well. So let’s all turn to the left and tell the next person all about it.

Comments
2 responses to “Chinese Whispers Graph Clustering in Python”
I encounter error when I trying your python code. Can you give me some advice?
—————————————————————————
KeyError Traceback (most recent call last)
in ()
19 for n, v in enumerate(nodes):
20 #G.nodes[n][‘class’] = v
—> 21 G.node[n][‘class’] = v
22
23 # run Chinese Whispers
/usr/lib/python3.6/site-packages/networkx/classes/reportviews.py in __getitem__(self, n)
176
177 def __getitem__(self, n):
–> 178 return self._nodes[n]
179
180 # Set methods
KeyError: 0
import networkx as nx
from random import shuffle as shuffle
…
for n, v in enumerate(nodes):
G.node[v[0]][‘class’] = v[1][‘attr1’]